Какова на самом деле "подпись художника" – Творца математики (если он был)

Заметки о главе 24 романа "Контакт" Карла Сагана, 1985.

Эти заметки философского характера написаны как реакция на указанную финальную главу романа "Контакт", где автор придумал не очень удачный вариант "подписи художника".

Но сама по себе эта неудачная авторская гипотеза не стоила бы обсуждения без того, чтобы привести пример более удачной гипотезы такого рода. Дело в том, что уже после издания романа, в математике было открыто нечто, что могло бы служить несравненно более подходящим примером для иллюстрации идеи автора, выраженной главной героиней романа – Элли (Элеонорой).

Так в чем эта идея?

Карл Саган, как и его героиня Элли, работал и был энтузиастом проекта SETI (Search For Extraterrestrial Intelligence). Суть проекта в постоянном прослушивании космоса на специальной радиочастоте, на которой естественный "шум" космоса близок к нулю, в надежде, что какая-либо удаленная цивилизация (внутри или даже за пределами нашей Галактики) пожелает рассылать по радио (!) какие-либо сведения для установления Контакта. Оставляя в стороне (не)реальность надежд на это, в романе такие сигналы не только были обнаружены и поняты, но и передали длиннейшую серию сообщений: односторонних сообщений (ибо об "обмене" сообщениями на расстоянии тысячи или даже миллионы световых лет не может быть и речи).

Согласно роману, это одностороннее послание в конце концов пересылает на землю детальнейший технический проект постройки некоей машины, принципы работы которой совершенно не понятны. Заявленная цель проекта – реализовать "путешествие" к его конструкторам для встречи с ними. И этим "путешественником" была Элли: ну, вернее, её нефизическая душа, ибо автор был достаточно аккуратен, чтобы его повесть грубо не нарушала законов физики.

И вот Элли (её душа), вернувшись на землю после общения с таким супер Разумом, и осознав Его невообразимую мощь, задумалась: а не мог ли такой Разум быть способен даже на то, чтобы сотворить математику по Его собственному проекту: сотворить – и оставить в ней свою "подпись", как художники делают на полотнах?

Элли решила, что "подпись" эту нужно искать в бесконечной дроби какого-либо важного в математике иррационального числа, скажем π. Книга кончается моментом, когда составленная ею компьютерная программа, обнаруживает в двоичной бесконечной дроби числа π такой сегмент, который легко интерпретируется как двоичная карта (bmp file) окружности! Этот грубый образ окружности, найденный в двоичном разложении π, так впечатлил Элли, что она увидела в нем "подпись Художника", "создавшего математику". Грубый контур окружности закодированный в π – это, прямо скажем, более, чем "скромное" представление о "подписи" подобающей гипотетическому Творцу математики. Ниже мы увидим, что существует подпись несравненно более впечатляющая, чем грубый контур окружности!

Разберем же идею о "подписи" более детально.

"Подпись художника?"

Сразу отметим, что метафора "подпись художника" в данном контексте не приемлема вообще. "Подпись" – это нечто произвольное. Художник может её поставить, или не поставить; подписать свое имя печатными или прописными буквами, или только инициалами. Иррациональное же число π определяется в математике как единственное решение определенных уравнений, или как (существующий, а потому единственный) предел определенных последовательностей. Не может существовать математики, в которой длина окружности единичного диаметра в Эвклидовой геометрии [1] отлична от уже известного значения π. Так, что никакой свободы "подписи" в числе π (или в некоторых иных "популярных" в математике иррациональных числах) быть не может.

Так можно ли "спасти" ожидания Элли обнаружив в математике "некий знак" от её творца? Можно ли открыть в математике некий сюрприз, совершенно шокирующий для человеческого исследователя математики (но, понятно, всегда известный подлинному её "создателю")?!

Дальнейший текст продемонстрирует существование такого шокирующего сюрприза, но мы должны будем перейти от метафоры "подписи" художника к другой метафоре, а именно…

Картины, допускающих две или более интерпретации.

Таких картин в истории живописи известно множество! Их различные (совершенно несвязанные!) интерпретации задуманы самими художниками, а от зрителя может требоваться некое умственное напряжение, чтобы "переключиться" с одной интерпретации на другую.

Применительно к математике, эта метафора имеет смысл попытки обнаружения какой-то еще не осознанной "картины" в известном объекте, может быть даже в числе π. Другими словами, речь идет о поиске какого-либо еще не известного вторичного свойства или вторичного назначения (double purpose feature) в уже известном математическом объекте, где вторичное назначение объекта есть следствие первичного, или утверждение эквивалентное первичному, или появление известного объекта в ранее неизвестном контексте. И таких ситуаций в математике уже известно множество. Вот пара простейших примеров.

Пусть первичное свойство состоит в задании множества чисел, делящихся на 3. Мы можем легко задать общий вид таких чисел n, где n = 3k (для любого натурального k). Однако, из элементарной арифметики известно и другое свойство множества чисел делимых на 3 (правда, имеющем место только в десятичной системе): сумма цифр чисел кратных 3, сама кратна числу 3 – и это есть вторично свойство, которое Элли могла бы с удивлением "обнаружить" (если бы не "привыкла" к нему еще в начальной школе).

Само число π было впервые определено древними греками в геометрии как предел определенной сходящейся последовательности, выражающей длину окружности диаметра 1. Однако веками позже, математики обнаружили, что число π возникает также контекстах не имеющих отношения к геометрии: например, как значение Гамма-функции Г(1/2) = √π . Гамма-функции – это распространение целочисленной функции факториал n! на действительные и комплексные числа. Какая взаимосвязь между длиной окружности и факториалом?!

Число π также появляется в определенных выражениях для ζ-функции Эйлера-Римана

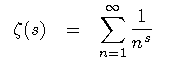
занимающей центральное место в теории чисел. Так, для четного аргумента 2k

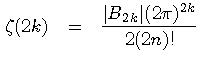
(где B₂_k это числа Бернулли). Также, имеет место соотношение

и число π появляется в сложнейших формулах, открытых Раманужаном. Какая взаимосвязь между длиной окружности, факториалом, и теорией чисел?!

Как тут не вспомнить разговор, которым открывается замечательная статья Вигнера [Wigner]:

– Это число π, – сказал статистик.

– Что это такое?

– Отношение длины окружности к ее диаметру.

– Ну, ты явно зашел слишком далеко в своей шутке. Наверняка численность населения не имеет никакого отношения к длине окружности.

Все это является иллюстрацией феномена о наличии в математике загадочных объектов вторичного и третичного назначения. Поэтому, "тайный знак" Создателя будем далее искать именно среди таких вторичных свойств.

Но сначала покончим с вопросом о том...

Что может быть "закодировано" в иррациональных числах.

Иррациональные числа были открыты ещё древними греками как числа, не представимые в форме дроби m/n при целых m и n. Греки доказали, что, например, √2 является иррациональным. В более поздние времена возникло эквивалентное определение иррациональных чисел как бесконечных десятичных (или в иной системе счисления) дробей, не имеющих периода (не представимых в виде повторяющихся сегментов цифр).

Есть два противоположных подхода к получению иррациональных чисел:

1. Построить некое иррациональное число с помощью заданного алгоритма без относительно к решению какой-либо задачи.

2. Решить некую задачу, у которой решение оказывается иррациональным числом.

Например, в случае (1), с помощью очевидного простого алгоритма можно построить иррациональное число a, бесконечная дробь которого есть последовательность s = {101001000100001.... }. Мы не знаем, обладает ли число а ещё каким-либо свойством, кроме как быть результатом заданного алгоритма.

Более того, в рамках такого подхода, легко составить иррациональное число, цифры которого кодируют любое желаемое сообщение, хоть целую Библию; или кодируют любое изображение. И уже после этих цифр добавить цифры последовательности s, что в совокупности тоже будет неким иррациональным числом.

Понятно, что подход (1), пригодный для кодирования чего угодно, не есть то, что интересовало Элли. Её интересовал именно подход (2), ибо π и ряд других "популярных" иррациональных чисел в математике возникают как решения специальных задач.

Например, алгебраическое иррациональное число √2 есть решение алгебраического уравнения x² = 2, е – решение неалгебраического уравнения ln x = 1, число ln 2 есть решение e^x = 2, π – одно из решений уравнения sin x = 0.

Как уже было сказано, π и другие вышеуказанные иррациональные числа являются единственными решениями соответствующих уравнений. Поэтому даже всемогущий Творец вселенной не обладает свободой изменить что-либо в единственном решении математической задачи. Мы же пытаемся понять, может ли последовательность цифр иррациональных решений ряда известных задач содержать некий информационный сегмент (специальный знак Творца) в качестве вторичного свойства этих решений.

Мы уже видели на примере последовательности s, что соответствующее иррациональное число содержит сегменты только одного определенного типа (а не любые), и только с цифрами 0 и 1.

С другой стороны, есть понятие нормального иррационального числа (по аналогии с нормальным распределением в теории вероятности). По определению, в нормальном иррациональном числе с базой b каждый сегмент цифр длиной n содержится с одной и той же вероятностью b⁻ⁿ (где b – база системы счисления). Такие числа существуют и построены. Согласно теореме Бореля, в нормальном числе любая желаемая последовательность когда-нибудь встретится с вероятностью 1. Для нормального иррационального числа, таким образом, желание Элли тривиально выполнимо для любого желаемого образа или последовательности цифр.

Проблема, однако в том, что ни для одного из популярных иррациональных чисел таких как √2, π, или e не доказано, являются ли они нормальными иррациональными числами (2024), хотя, судя по компьютерным экспериментам, они похожи на таковые. Но если это так, то число π содержит где-то в своем разложении любой образ или любое желаемое сообщение, а также его отрицание, и его версии с грамматическими ошибками... Не говоря уже о том, что "где-то" в бесконечной последовательности означает сколь угодно далеко. Однако никогда и ни на каком компьютере не удастся довести поиск далее, чем, скажем 10⁵⁰ цифр.

Таким образом, сама затея Элли по обнаружению в π какого-либо специального графического образа-знака от Создателя математики не имела смысла.

А где ещё в математике есть смысл искать какие-либо объекты вторичного назначения в виде графического образа?

Скатерть Улама

Простые числа и законы их распределения – это старейшая тема математики, в которой по сей день есть нерешенные проблемы. Если обозначить на прямой черными точками положение простых чисел, то мы увидим, что они встречаются всё реже и реже, но распределены нерегулярно, и в каком-то смысле "случайно". Ибо, хотя простые числа расположены все реже и реже (в соответствие с уже известными асимптотическими оценками), тем не менее, на любом расстоянии от начала попадаются, простые близнецы[2], т.е. пары, отличающиеся всего на 2 (или пары, отличающиеся на 4). Именно такие пары близких простых среди все более редко встречающихся остальных простых, создают впечатление случайности в их распределении на прямой.

Однако, если нанести натуральные числа не на прямую, а на плоскость каким-либо регулярным образом, обозначив коричневым простые из них, то нас ожидает сюрприз, называемый скатерть Улама [Ulam].

Скатерть Улама (источник - Википедия).

Регулярное нанесение на плоскость может быть либо вдоль архимедовой спирали, либо вдоль "квадратной спирали". Сюрприз же состоит в том, что точки простых чисел на этой скатерти окажутся расположенными примерно с одной плотностью (а не как на прямой), и в их узоре будут явно заметны отрезки прямых линий!

Этот феномен концентрации простых чисел на отрезках в скатерти Улама объясняется другим феноменом, открытым еще Эйлером. Оказывается, некоторые квадратные трехчлены генерируют простые числа в количестве выше, чем другие полиномы. Таков, например, квадратный трехчлен Эйлера n² – n + 41, выдающий простые числа для n = 1, ..., 40.

Когда натуральные числа нанесены на плоскость вдоль одной из указанных спиралей, то точки, находящиеся на диагоналях, принадлежат всевозможным квадратным полиномам так, что те из полиномов, которые обильно генерируют простые числа, создают эффект отрезков, насыщенных простыми числами.

Отрезков, заполненных простыми точками плотно, в скатерти Улама нет, но сам факт их концентрации на отрезках прямых удивителен и вполне мог бы быть подходящим кандидатом на "особый сигнал", о котором мечтала Элли (и Саган), не менее, чем образ окружности в цифрах числа π.

Но самый подходящий и удивительный претендент на особый сигнал – это...

Фракталы и множество Мандельброта.

Сейчас я попытаюсь продемонстрировать, что графический образ множество Мандельброта [Mandelbrot] – это наиболее яркий особый сигнал, о котором Элли и Саган могли только мечтать!

Если взглянуть на картинку множества Мандельброта не сильно присматриваясь,

Рис. 1. Множество Мандельброта (источник - Википедия).

то с первого взгляда она покажется мало чем отличающейся от картинок других хорошо известных множеств, границы которых задаются какими-либо алгебраическими уравнениями (ниже).

Например, единичная окружность задается уравнением х² + у² = 1, а точки соответствующего диска – неравенством х² + у² < 1.

А уравнение у = ± (1 – х²)^1/2 + х^2/3 задает "сердечко".

Границы множеств, заданных алгебраическими уравнениями, есть "простые" алгебраические кусочно-гладкие кривые. Отметим этот факт.

Множество Мандельброта М определяется тоже с помощью простейшего алгебраического уравнения на комплексной плоскости с тем лишь отличием, что критерий принадлежности к множеству определен не выполнением неравенства, а фактом ограниченности или неограниченности некоторой итерационной последовательности, основанной на заданном алгебраическом уравнении.

А именно, пробная точка комплексной плоскости c принадлежит М если итерационная последовательность {z_n}

z_n₊₁ = z_n² + c, z₀ = 0, n = 0, 1, 2, ....

ограничена, и c не принадлежит М в противном случае.

Оказалось, что граница множества М не является простой кусочно-гладкой кривой конечной длины, как в примерах выше. Если мы внимательно присмотримся к статической картинке множества Рис. 1, то заметим, что его контур, издалека похожий на кардиоиду, содержит ряд выступов разных размеров. При дальнейшем увеличение оказывается, что каждый из выступов в свою очередь содержит всевозможные "кренделя" и завитушки, в чем-то похожие, но не точно подобные предыдущим. С помощью компьютера, можно продолжать "всматриваться" в каждую из деталей при всё возрастающем увеличении обнаруживая, новые и новые вензеля и детали: и так до бесконечности.

Множество Мандельброта

в процессе бесконечного увеличения (источник - Википедия)

Границы такой бесконечно сложной структуры называются фракталами.

Множество Мандельброта обладает еще длинным списком свойств (см. Википедию), в одном из которых возникает ...

Возникает число π! (Элли, где ты?!)

И вот теперь, с трепетом осознав всю бесконечную сложность и красоту множества Мандельброта, этой чисто абстрактной и с виду столь простой конструкции, остается процитировать слова Сэра Роджера Пенроуза:

"Эта абстракция присутствует, существует, и является реальностью не менее, чем гора Эверест, и подлежит исследованию также, как и неизвестные джунгли." [Penrose]

Не это ли и есть тот потрясающий "знак" от Создателя математики, который искала Элли?!

Нужно отметить, наконец, что множество Мандельброта – это отнюдь не единственный ныне известный фрактал. Помимо того, что оно первое из подобных фракталов, множество М удобно для изучения ещё и потому, что для него существует простой критерий ограниченности последовательности (чего нет для иных более сложных множеств).

И в заключение, давайте пофилософствуем немного.

Может ли у математики быть Создатель?

Это вовсе не само собой разумеется, что "законы природы" вообще существуют, и тем более, что человек способен их познавать. (Э. Шрёдингер)

Непостижимая эффективность языка математики для формулировки законов физики – это чудесный дар, который мы не понимаем и не заслуживаем. Мы должны испытывать благодарность за этот дар. (Ю. Вигнер)

Чтобы рассуждать на эту тему, нужно признать ту или иную из существующих философских аксиоматик касательно того, из чего состоит всё сущее. В дуализме, например, признают существование Физического (материального) мира, плюс мира Абстракций или идей, т.е. Платоновской вселенной. (Я придерживаюсь концепции триализма, что существует еще и третья компонента – мир Сознания и Души).

Так вот, математика, как отмечал Роджер Пенроуз, это особый раздел вселенной Платона, и вот в каком смысле. Платоновская вселенная (по аналогии с интернетом) содержит всё что угодно, теории правильные и неправильные, правду и ложь, последовательности, имеющие смысл, и не имеющие.

Но среди всего этого только математика является абсолютной истиной в море прочих произвольных абстракций платонической вселенной.

· Математика, будучи системой чистых абстракций, "находится" совершенно вне физического мира так, что ни одно понятие математики не обнаруживается в физическом мире. Однако при этом...

· Имеет место непостижимая эффективность математики в естественных науках [Wigner] состоящая в том, что математические абстракции, тем не менее, пригодны для моделирования физического мира, хотя и приближенно! Не потому ли это имеет место, что Создатель физического мира проектировал Своё творение применяя математику?

· В отличие от мира физического, у математики не могло быть момента возникновения. Математика существует не зависимо от физического мира, а также не зависимо от того, есть ли человек, или какой-либо иной разум, который пытается её познать. Более того...

· В отличие от физического мира, математика не могла быть "создана", ибо акт создания подразумевает, что Создатель рассматривает разные "возможные" варианты и останавливается на одном из них. Однако, математические истины не могут быть многовариантными. Не может быть такого варианта математики, в котором, скажем, количество простых чисел конечно. Или решение уравнения, имеющего единственное решение, стало другим. Или некий объект вторичного назначения перестал быть таковым, скажем Г(1/2) ≠ √π .

· И последнее: сама же математика (теорема Гёделя) утверждает, что существуют такие математические утверждения, истинность которых не может быть доказана никаким конечным доказательством. Поэтому такие утверждения для человека всегда будут открытыми и непроверяемыми.

Вышеперечисленный набор характеристик может быть присущ только самому Творцу вселенной, который, как и математика, существует вне физического мира и существует всегда. Если согласно философии Августина математика – это часть вечной истины Бога, то я рассматриваю математику как часть разума самого Бога.

Alexander Gofen

2024

Литература

[Wigner] Eugene Wigner "The Unreasonable Effectiveness of Mathematics in the Natural Sciences"

Непостижимая эффективность математики в естественных науках

https://www.hep.upenn.edu/~johnda/Papers/wignerUnreasonableEffectiveness.pdf (in English)

Карл Саган. Контакт (на русском)

http://www.lib.ru/INOFANT/SAGAN/contact.txt

[Ulam] https://en.wikipedia.org/wiki/Ulam_spiral

[Mandelbrot] https://en.wikipedia.org/wiki/Mandelbrot_set

[Penrose] Roger Penrose, "The Emperor's New Mind", 1989.

[1] В геометрии на сфере радиуса r, например, "диаметр" большого круга на поверхности сферы (т.е. полу меридиан) есть πr, а длина окружности большого круга (т.е. экватора) 2πr. Однако, известная величина π определена именно для Эвклидовой геометрии и именно для окружности на Евклидовой плоскости.

[2] Так, вначале мы имеем пары (3, 5), (5, 7), ..., (29, 31). А самая большая (2022) уже найденная пара близнецов – это 2996863034895 × 2^1290000 ± 1. Пока не известно, является ли множество близнецов конечным или бесконечным.