Applications of the Taylor Center software
for teaching and research
This page reviews a few articles which demonstrate how this software
may be used for teaching and research purposes due to its particular
features such as...
- Availability of Taylor expansions and n-order derivatives of the
solution;
- Real time animation of the motion along the
trajectories in 2D
and 3D;
- Plotting phase portraits and families of
Initial Value Problems,
and others.
The software by itself comes with a file of scripts demonstrating
many illustrative problems from Geometry (such as the Möbius surface outline) to
a variety of celestial mechanics problems and basic mechanics problems
such a pendulums (in folder Samples
and under menu Demo). For
each of these pre-loaded classical problems you will find suggested
didactical comments below, or a teacher can provide own comments
and explanation, as well as to add many other illustrative problems of
his own interest.
Articles on application
of the Taylor Center software for teaching
The three articles below exemplify various teaching ideas and topics
for which the Taylor Center software happened to be beneficial or
indispensable.
This article addressed a variety of topics beginning with the most
straightforward feature...
* Visualization of dynamics via real
time drawing. A selection of the analyzed examples are...
- A chemical reaction (a "vine glass" - credit to the
late Prof. Borrelli);
- Double pendulum with its chaotic movement;
- Other illustrative examples offered in the Demo menu and Script files, including...
- The Lagrange case of the Three-body problem, used as a
platform for and demonstration for a few other related topics such
as...
- Instability of the Lagrange case (demonstration of a
beautiful disturbed case) in 2D and 3D;
- Choreography of n-body problem;
- Posing a question whether an analogue of the Lagrange case
is possible in 3 dimensions on the vertices of the classical 5 regular
polyhedra rather than on the regular polygons in 2 dimensions. The
answer is No, and the proof is provided in the Appendix
* Studying properties of the
Taylor expansions...
- Behavior of the Taylor terms as the bell shape, visualized
in the Dynamic Profile Diagrams demonstrating how the step affects the
bulge;
- Heuristic and true convergence radii. How the program
compute them and behaves for in case of a finite and infinite
convergence radius;
* Is the highest accuracy in the
Taylor method always achievable? An in-depth discussion of the
types of numerical error and their sources, particularly the so called
cancellation of subtraction catastrophic error.
* Regular solutions of singular ODEs.
This chapter brings and explains the idea that sometimes a regular
holomorphic solution may satisfy ODEs having singularity at the point
where the solution is regular. Moreover, in some functions
there are regular points at which the function may satisfy
only singular ODEs (in the class of rational or elementary ODEs). The
demo role of the program is based on its feature to cope with ODEs
having an isolated point of singularity which however is a regular
point for the solution.
* Weird examples of real valued solutions vs. their complex properties.
Here (among others) is analyzed the function cos(sqrt(t)) which is regular at t=0 (when properly defined). It is
explained how to integrate and plot this function for t<0 despite that it involves
complex values.
Gofen, Alexander (2012) "Using the Taylor Center to Teach ODEs,"
CODEE Journal: Vol. 9, Article 6.
Available at: http://scholarship.claremont.edu/codee/vol9/iss1/6
This articled was prompted by a real life situation, when the authors
used the Taylor Center for plotting the solution of a suggested by
somebody system of ODEs (not yet knowing the origin of these equations):
x' = x² – y²+
2xy – x – 3.5y +
1, x(0)=0.1
y' = -x² + y² + 2xy – y + 3.5x – 1,
y(0)=0
The graph of the solution was plotted
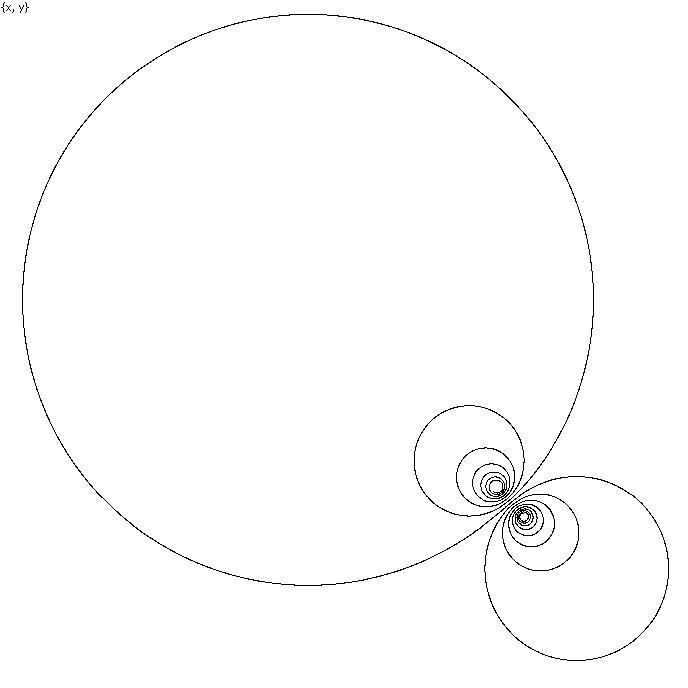
however what attracted attention of the authors was a remarkable
dynamic of evolution of this double spiral, animated by the program in
real time. It seemed that each loop of the double spiral (no matter big
or small) took the same time to run! (See this example under Demo/Spirals/Double spiral). The
program allowed to accurately compute the time spans taken by the loops
- and they
happened to be equal (up to the rounding error), confirming that the
initial impression was based on the reality.
This remarkable property (figured out by mere observation of the
dynamics of drawing) doubled up my interest for examining the origin
and properties of this system, which happened to be a real valued form
of a complex ODE
z'
= (1 – i)z² + (-1 +
3.5i)z + 1 –
i, z = x + iy
representing the turned complex tangent function. On an
intuitive level this fact immediately clarified the source of this
remarkable time periodicity in the spiral loop, however it took certain
efforts to prove this and a few other unexpected properties of the
solutions of such systems.
Therefore this research exemplifies a mathematical study triggered
by observation of numerical experiments at a computer, followed by the
conventional mathematical analysis of the observed phenomenon. Not only
did this mathematical analysis succeed in establishing the proof and
explanation for what was observed, but it also revealed existence of
the critical asymptotic curve. This curve
would have been impossible to find by numerical experiment only. The
numerical experimenting and the analytic approaches complemented each
other beautifully in discovering a remarkable property of a particular
planar polynomial system of ODEs - presenting a powerful teaching
moment.
This paper is dedicated to the two classical transcendental functions:
The locus of points for which powers commute, and the locus of points
for which powers associate. These classical functions however are
considered in a new perspective: as holomorphic
solutions of ODEs yet passing over the points of singularity of these ODEs.
For example, for the function y(x)
of commuting powers defined by the equation xy=yx, we
obtained also ODEs satisfied by y(x)
y/x – ln y
y' = ––––––––
x/y – ln x
or
y"x2y2(y – x) – (y')3x4 + (y')2yx2(3x – 2y) + y'y2x(3y – 2x) – y4 = 0 .
Both ODEs have a singular point at (e,e)
though the solution y(x) is holomorphic at this point. In order to
obtain the Taylor expansion for y(x) at (e,e) the standard AD formulas are not
applicable because of the singularity of these ODEs, so that the Taylor
coefficients at this point must be obtained via special recursive formulas. As soon as
these coefficients are available, the Taylor Center becomes helpful due
to its capability to start integration even at a singular point of the
ODEs if the solution is regular at this point and the special Taylor
expansion of the solution is provided (from other sources). Thanks to
this feature, the software can deal with the special ODEs studied here
and pre-loaded into the distribution package so that the users can
reproduce all the graphs referred in this article.
Published in: Teaching Mathematics and Computer Science, 11/2,
2013, p. 241-254.
Exploratorium
(didactical
comments for the preloaded problems)
The software comes with the
folder Samples containing
numerous ready to use samples of Initial Value
Problems (IVPs) helpful for teaching.
The selection of the samples
covers various branches of applied mathematics: from purely parametric
curves
(where the ODE section contains merely a trivial ODE t'=1) to many
samples in celestial mechanics, general mechanics (single and double
pendulums,
rolling disk), examples of special functions such as the Bessel
function (which
are regular, but their ODEs are singular), and some others. Here is the list
and minimal explanations for several hundreds samples pre-loaded with
the program including ...
- Exploratorium
of Choreograhies for the planar Newtonian 3-body problem with equal
masses, where you will find the explanation of the concept, the
resources, and
how to run 345 samples of Choreographies kindly submitted by Prof.
Carles Simò.
-
Exploratorium of periodic
solutions recently discovered for the planar Newtonian 3-body
problem with equal masses. The first colletion of 203
represents closed curves
whose initial vectors were kindly provided thanks to Ana Hudomal. The second collection
of 30 samples are the cases where the periods are represented with finite curved segments at whose
extremes the bodies have zero velocities (i.e. they are in a free fall)
- thanks to the data by Xiaoming
LI and Shijun LIAO.
-
The workshop about new properties of the free fall periodic
orbits (Gofen).
The full description for all
them (called Exploratorium) is in preparation.
Examples
of applications and
articles in scientific Delphi with a teaching potential
1. From
Pascal to Delphi to Object
Pascal-2000. ACM
SIGPLAN Notices, Vol. 36, No. 6, pp. 38-49 (2001).
2. Object vs. Class:
Fewer Pointers, Less Double Thinking. Delphi
Informant Magazine, Vol. 5, No. 7, pp. 47-52 (1999).
An in-depth discussion about the direct (one-to-one
mapped) variables vs. indirect and separated reference to variables in
programming languages.
3. Dynamic Arrays.
Delphi Informant Magazine, Vol. 6, No. 2,
(2000).
An evolution of the concept "dynamic array" from
ALGOL-60 to Delphi
4. Recursion Excursion.
Delphi Informant Magazine,
Vol. 6,
No. 8, pp. 30-38 (2000).
Theory and examples of code on:
- parsing of
arithmetic expressions into a Reverse Polish notation (RPN);
- recursive
evalutation of the PRN;
- a code of an
advanced calculator of expressions.
5. A Recursive Journey
to the Problem of Three Bodies. Delphi
Informant Magazine. Vol. 8, No. 3, pp.
44-49, (2002)
Theory and examples of code on:
- parsing of
arithmetic expressions into a Reverse Polish
notation (RPN);
- compiling
RPN into a list of Automatic Differentiation (AD) instructions;
- a software
emulator of the AD processor processing the list of AD instructions.
6. 3D Delphi:
Stereo Vision on Your Home PC. Delphi
Informant Magazine. Vol. 10, No. 1, pp.
8-15, (2004)
7. Do-It-Yourself 3D. Delphi
Informant Magazine. Vol. 10, No. 8, pp. 17-22, (2004)
Theory and examples of code on:
- geometry of
stereo pair;
- anagliph
(red/blue) technique of viewing stereo pair;
- implementation
of the red/blue technique of viewing stereo pair using the
graphic power of Delphi.
More
topics with teaching potential contained in the Taylor Center software
- The algorithm of plotting parametric 2D and 3D curves point
by point based on their Taylor expansions guaranteeing their
continuity.
- The algorithm of tube-like
plotting 3D curves with resolution of skewing controversies in
3D stereo and in isometric plotting.
- The algorithm of real time
playing trajectories according to their parametric
representation as functions of time.
- The algorithm for obtaining ODEs in another state (in
another independent variable) and switching the integration from one
independent variable to another.
